こんにちは,はじめまして,9月からAIチームにジョインした下山と申します.
本記事はAI Shift Advent Calendar 2021 7日目の記事です.
本記事では,New York University & Spotify が発表した,介入割当手法の性能比較に関する研究[1]の紹介を行います.
はじめに:本研究に興味を持った理由
現在,AI Shiftでは機械学習モデルや様々なパラメータ(これらをまとめて介入と呼ぶことにします)がビジネスに与える影響を評価し,より良い介入の決定・仮説検証を行うためにA/Bテストシステムの開発を行なっています.
A/Bテストを行うと,(特徴量, 割り当てられた介入, 評価値)の3つ組みが得られます.
基本的には,このデータは,最も評価値の良い介入の選択(割り当てられた介入毎に評価値の平均を計算して行う)・事前に立てた仮説の検証に用いられます.
しかし,せっかく特徴量もセットで得られるので,仮説検証に使っておしまいではなく,よりサービスをグロースさせられる使い方ができると良さそうです.
そこで,この3つ組を眺めていると次のような発想が生まれるかと思います:どのユーザ(i.e. 特徴量)に,どの介入を割り当てたら,最も評価値が高くなるか?を決定する機械学習モデルを作ればより性能が高いモデルができそう.
実際,上のような機械学習による介入割当に関する研究は多く行われています.
今回紹介する研究[1]は,介入割当の方法3種類を解析的・実験的に比較した研究になります.
研究紹介
以降で研究[1]の紹介を行います.
本記事では,大きく以下2つの章立てで紹介します:
・介入割当方法3種類とそれらの違いについて,
・実システムを用いた,それら3種類の比較実験の結果について.
notation
\(\mathbb{R}, \mathbb{N}\): それぞれ,実数全体,自然数全体の集合.自然数には \(0\) を含めないとする.
\(X \in \mathbb{R}^d\): 特徴量(e.g. ユーザ属性,事前にクリックした商品)
\(Y \in \mathbb{R}\): アウトカム(i.e. 最適化したい評価値.e.g. 1ユーザあたりの商品購入数)
\(T \in \{1, 2, \ldots, K\}\) : 介入(アウトカムを最適化するために変更する変数.e.g. 機械学習モデル,クーポンを配る)
\(K \in {\mathbb{N}} \): 介入種類数
3種類の介入割当方法とその違い
介入割当とは,介入効果の期待値が最も高くなる介入を選択する問題です.
つまり,アウトカムの条件付き平均$$ \mu(x, k) = E\left[Y|X=x, T=k\right] $$に対して,その差$$\tau(x,k) = \mu(x, k) - \mu(x, 0)$$が最大となる介入 \(k \in \{1, 2, \ldots, K\}\) を各 \(x \in X\) に対して選択する問題です.
ここで,\(T=0\) はベースラインの介入を表し(e.g. 現状動いているアルゴリズム),\(\tau(x,k)\) が介入 \(T=k\) の介入効果を表します.
直感的には,特徴量がユーザを表すとすると,\(\tau(x,k)\) はユーザ \(x\) に対し介入 \(T=k\) を割り当てるとベースラインよりどのぐらいアウトカムが変化するかを表しています.
これまでに,機械学習モデルに基づいた介入割当手法がいくつも提案されていますが[2][3][4][5],研究[1]ではこれらを被推定量(予測変数)に応じて次の3種類に大別しています:
- Outcome prediction (OP),
- Causal effect prediction (CP),
- Optimal assignment prediction (AP).
3種類の方法が用いる被推定量,介入の選択方法を表1にまとめました.
ここで,記号 "^" はモデルによる予測を表しています.
| 方法 | 被推定量 | 介入の選択方法 |
| OP | \( \mu(x, k) \) | \(\mathop{\rm arg~max}\limits_k \hat{\mu}(x,k)\) |
| CP | \( \tau(x, k) \) | \(\mathop{\rm arg~max}\limits_k \hat{\tau}(x, k)\) |
| AP | \(a^\ast(x) = \mathop{\rm arg~max}\limits_k \tau(x, k)\) | \( \hat{a}^\ast (x) \) |
OPは,アウトカムの平均を予測し,それが最大となる介入を選択します.
CPは,介入効果を予測し,それが最大となる介入を選択します.
APは,介入効果が最大となる選択自体を学習します.
CPとAPの違いが少し分かりづらいかもしれませんが,クラス分類において,クラスに属する確率を予測する(これがCP)か属するクラス自体を予測するか(これがAP)の違いと考えると分かりやすいかもしれません.
3つの方法はいずれも理想的な条件(データが十分多く,機械学習モデルのパラメータ推定量が一致推定量)を満たせば漸近的に最適な割当を得ることができることが示されているそうです[1].
しかし,実問題においては,得られるデータ数は有限であるためこれら3つの方法に違いが生じます.
その1つとして,「OP・CPは予測性能が介入割当の性能と必ずしも一致しない」事が挙げられます.
OP・CPは予測性能と介入割当性能が必ずしも一致しない
この問題は損失関数によって引き起こされます.
OPは,アウトカムの平均を予測するため,以下の二乗誤差損失関数が用いられます:$$ E_{Y, X}\left[ \left(Y - \hat{\mu}(X, k) \right)^2 \middle| T=k \right]. $$つまり,機械学習モデル \( \hat{\mu}(X, k) \) がアウトカム \(Y\) をなるべく上手く予測できるように学習します.
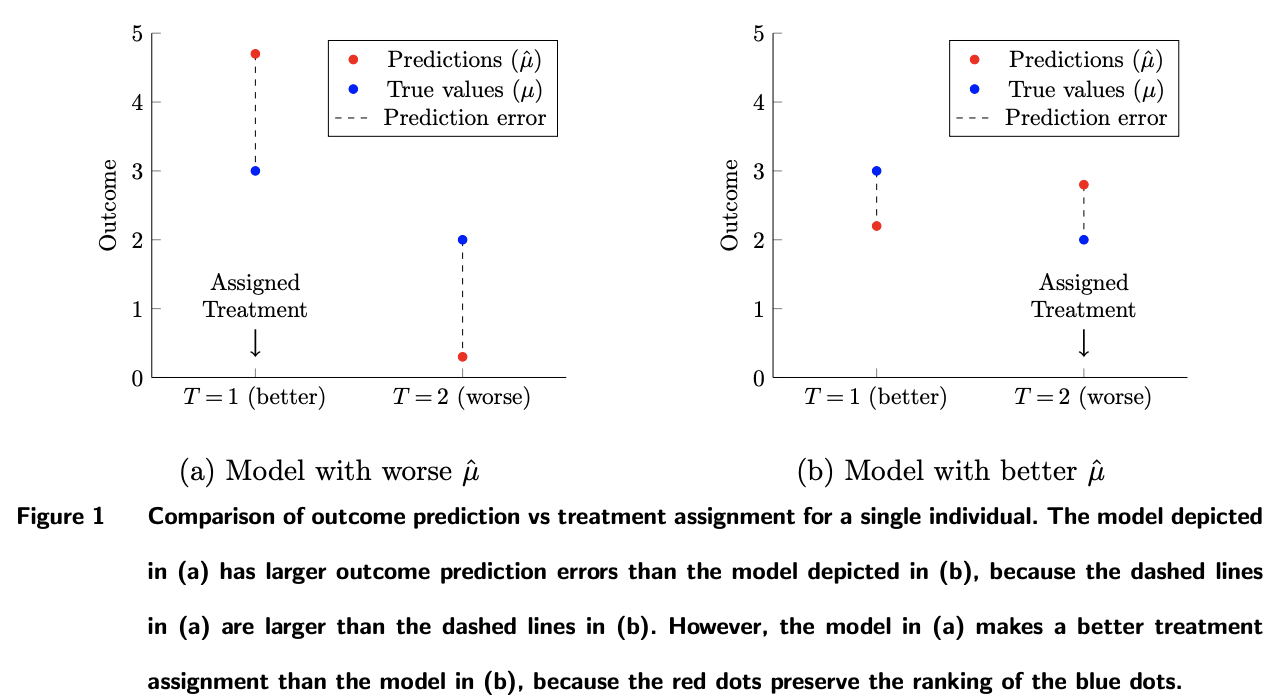
この学習方法により,図1(上図)のような問題が生じます.
(a), (b)はそれぞれ異なる予測モデル \(\hat{\mu}\) の結果を表しており,青丸が各介入における真のアウトカム平均,赤丸が各介入におけるモデルの予測値を表しています.ここでは,簡単のため特徴量 \(X\) は定数とし省略しています.
予測モデルの性能としては(b) > (a)です(∵ 真の値と予測値のズレが(b)のモデルの方が小さい).
一方,介入割当の性能は(a) > (b)です(∵ 真の値は\(\mu(T=1) > \mu(T=2) \)なので介入として \(T=1\) を選択すべき.ところが,(b)は \(\hat{\mu}(T=1) < \hat{\mu}(T=2) \) と予測しており,介入 \(T=2\) を選択してしまう).
CPでも同様の問題が生じます.
CPは,介入効果を予測するため,以下の二乗誤差損失関数が用いられます:$$ E_{X, Y(0), Y(k)}\left[ \left( Y(k)\ - Y(0)\ - \hat{\tau}(X, k) \right)^2 \right]. $$ここで,\(Y(k)\) は介入 \(T=k\) が割り当てられた場合のアウトカムを表します.
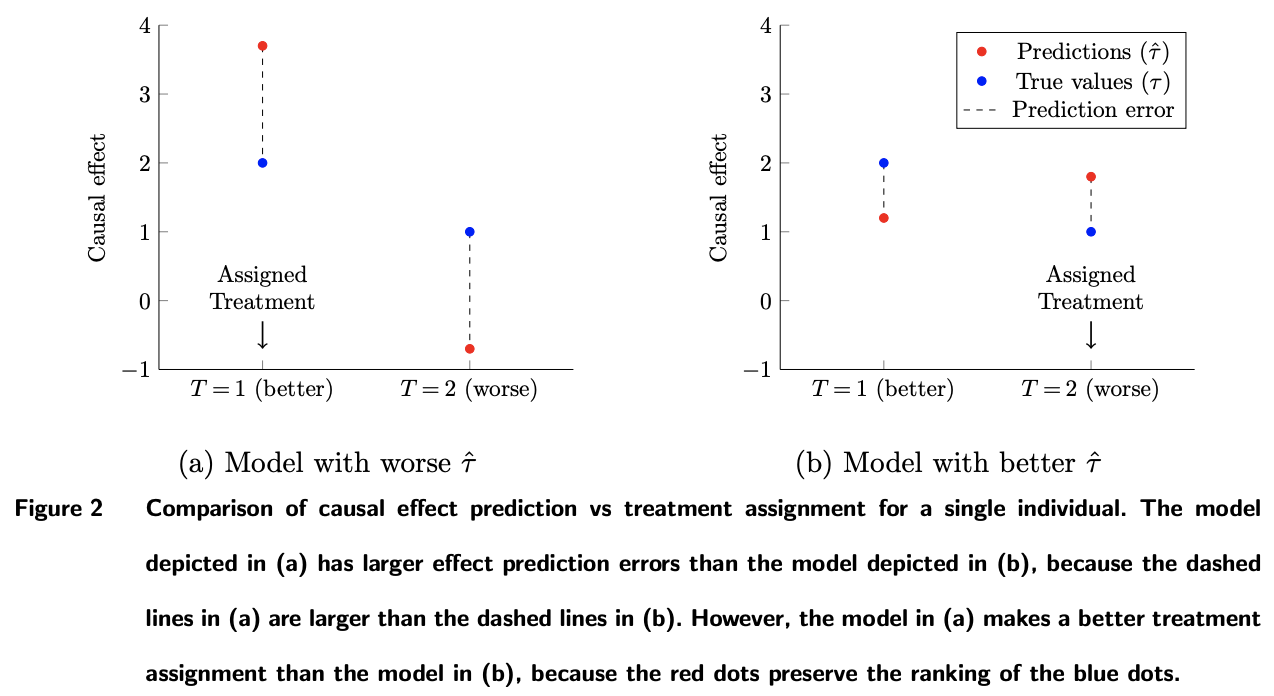
図2(上図)は図1と同様の問題を表しています.
縦軸が介入効果,モデルが介入効果予測モデル \(\hat{\tau}\) になっています.
伝えたいことは図1と同様です.
このように,OP・CPは最適な割り当てを学習できない場合があるということがわかりました.
OP・CP・APの違いが実問題においてどの程度の差を生むのかを次の章で見てみます.
実システムを用いた3方法比較実験
研究[1]では,Spotify の実システムで行ったA/Bテストで得られたデータを用いて,3手法の性能を評価しています.
アウトカムは,1ユーザあたりの総再生回数です.
データ
4つのplaylist生成アルゴリズム(1つはベースライン介入,残り3つが比較介入)でA/Bテストを行なって得られた3つ組(ユーザの特徴量,割り当てられた介入,総再生回数)のデータを使っています.
データ数は全部で770millionであり,各介入におけるデータ数の比率はベースライン86.68%,そのほか3つがそれぞれ4.44%です.
特徴量として,5種類のカテゴリカル変数を用いています.
one-hot encoding した場合,各カテゴリ変数の次元はそれぞれ 3, 19, 6, 8, 4 です.
評価方法
次の4手法を比較しています:
・アウトカムの平均が最も高い介入(i.e. \( \mathop{\rm arg~max}\limits_kE\left[Y | T=k\right]\) )を全ユーザに割当
・OPを用いて介入を割当,
・CPを用いて介入を割当,
・APを用いて介入を割当.
OP・CP・APは全て,tree-basedモデルを用いて予測モデルを構築しています.
A/Bテストで得られたデータを学習データ・テストデータに分けて評価しています.
評価指標は,ベースライン介入を割り当てた場合と比較して再生回数が増加した割合です.
検証には10-fold nested cross validationを用いています.
(以下の内容は論文内には書いておらず,私の推測になります.)
このようにデータを分割すると,ある \(X=x\) に対して介入 \(T=k\) を割り当てたデータがテストデータに存在せず,モデルが割り当てた介入を評価できない場合が存在するのではないかと考えられます.
ただ,単純計算したところその可能性は少なそうです.
one-hot encodingした場合の各カテゴリ変数の次元数から,単純計算すると,\(X\) が取りうる値のバリエーション数は 10,940 です.
よって,介入 \(T=k\) が割り当てられたユーザ数 ÷ 10940で,特徴量 \(X=x\) かつ介入 \(T=k\) が割り当てられたユーザ数(データ数)を求めると
・\( k=0 \) : 約6万
・\( k\neq 0\) : 約3千
となります.
全体のデータ数が770millionと十分に存在するため,特徴量かつ介入でセグメント分けしても各セグメントに一定のデータは存在していそうです.
実験結果
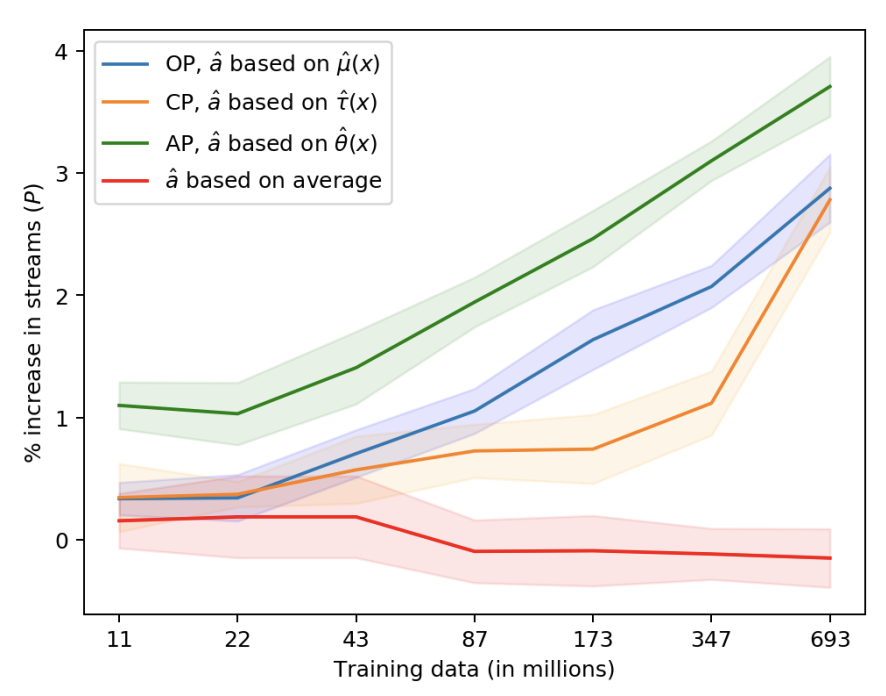
上図は比較した4手法の学習データ数に対する評価指標の推移を表しています.
影はcross validationの結果から計算した95%信頼区間です.
この結果から大きく次の3つが分かります:
- APはOP・CPと比較して良好な性能を示している.
- 全ユーザに同じ介入を割り当てるより,ユーザ毎に適切な介入を割当てる方がアウトカムが向上する.
- 学習データが増加するにつれ予測モデルを用いた場合のアウトカムが向上する
実際,上図から,AP(緑)はOP(青)・CP(オレンジ)より良好な性能を示していることが分かります.
また,全ユーザに同一の介入を割当てる(赤)より,ユーザ毎に適切な介入を割当てる(緑,青,オレンジ)方が良いことも分かります.
(通常,A/Bテストでは,赤の方法,つまりアウトカムが最も高い介入を選択します.i.e. \( \mathop{\rm arg~max}\limits_kE\left[Y | T=k\right]\).これを見るとA/Bテストで棄却した介入の中にも,特定のユーザに対しては効果の高い介入が眠っているかもしれません. )
最後に,データ数が増加するにつれて介入選択モデルを用いた場合の評価指標が向上していますが,これは各 \(x \in X, k \in \{1, 2, \ldots, K\}\) に対し,特徴量 \(X=x\) かつ介入 \(T=k\) が割り当てられたユーザ数(i.e. 各セグメントにおけるデータ数)が増加するのでモデルの性能を向上させることができるためであると述べられています[1].
終わりに
今回は New York University & Spotify から発表された研究[1]についてまとめました.
介入割当方法を大別しそれらの違いをまとめていることに加え,実データを用いた検証によりその違いの影響を評価しており,個人的にはとても勉強になる研究でした.
AI Shiftにおいても,音声自動対応サービスにおいて,ユーザ毎に最適なパラメータを選択するモデルを組み込むことでユーザ一人一人に適した音声対応を実現しユーザ体験をより高めることができるのではないかと考えられます.
本記事では紹介できなかった内容(e.g. OP, CP, APそれぞれに関する既存研究,予測モデルとしてtree-base以外を使った場合の性能比較)についても詳しく言及されているので,ご興味のある方は一度原論文を読んで見られると良いかもしれません.
明日はTorchArrowに関する記事が出ますので,そちらも是非ご一読していただければと思います.
最後まで読んでいただきありがとうございました.
参考文献
[1] Carlos Fernandez-Lorıa, et al. 2021. A Comparison of Methods for Treatment Assignment with an Application to Playlist Generation. arXiv
preprint arXiv:2004.11532 (2021).
[2] Baqun Zhang, Anastasios A Tsiatis, Marie Davidian, Min Zhang, and Eric Laber. 2012. Estimating optimal treatment regimes from a classification perspective. Stat 1, 1 (2012), 103–114.
[3] Kathleen Kane, Victor SY Lo, and Jane Zheng. 2014. Mining for the truly responsive customers and prospects using true-lift modeling: Comparison of new and existing methods. Journal of Marketing Analytics 2,
4 (2014), 218–238.
[4] Stefan Wager and Susan Athey. 2018. Estimation and inference of heterogeneous treatment effects using random forests. J. Amer. Statist. Assoc. 113, 523 (2018), 1228–1242.
[5] Susan Athey and Stefan Wager. 2021. Policy learning with observational data. Econometrica 89, 1 (2021), 133–161.






