はじめに
こんにちは,AIチームの下山です.
本記事は AI Shift Advent Calendar 2022 の24日目の記事です.
前回の記事で可測空間・測度・可測写像についての基本的な性質を扱ったので,本記事では,その続きとして,測度を用いた可測関数の積分について紹介します.
本文
記号
利便性のため,いくつか記号を導入します.
- \((S, \mathscr{A}, \mu)\): 測度空間
- \( \mathbb{M}(S \to [0, \infty))\): \(S\) から \([0, \infty)\) への \(\mathscr{A}/\mathscr{B}([0, \infty))\)-可測写像全体の集合
- \( \mathbb{M}(S \to \mathbb{R})\): \(S\) から \(\mathbb{R}\) への \(\mathscr{A}/\mathscr{B}(\mathbb{R})\)-可測写像全体の集合
- \( \mathbb{S}(S \to [0, \infty))\): \(S\) から \([0, \infty)\) への非負単関数全体の集合
以降,本記事では,測度空間 \((S, \mathscr{A}, \mu)\) が1つ任意に固定されているとしておきます.
非負単関数の積分
非負単関数の積分を以下で定義します.
定義1. (非負単関数の積分) \( h \in \mathbb{S}(S \to [0, \infty)), A \in \mathscr{A} \) とする. \(h\) の 測度 \(\mu\) による \(A\) 上の積分を以下で定義する: \( \int_A h d\mu := \sum_{n=1}^N a_n \mu(A_n \cap A)\) ここで,\(h = \sum_{n=1}^N a_n 1_{A_N}, \{a_n\}_{n=1}^N \subset [0, \infty), \{A_n\}_{n=1}^N \subset \mathscr{A}\ \text{s.t.}\ S = \sum_{n=1}^N A_n \).
上の定義は 非負単関数の表示の仕方に対して,well-defined である.
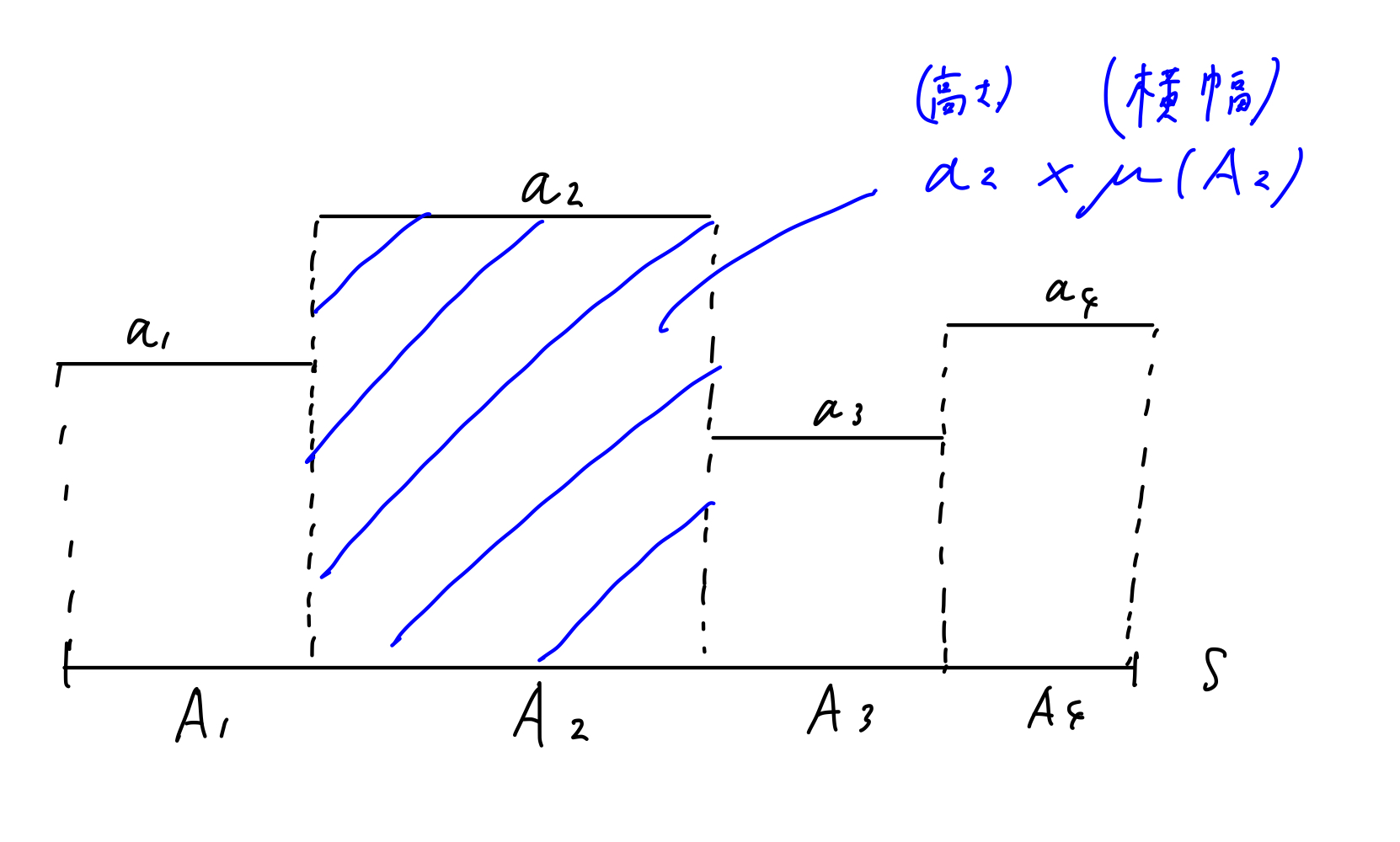
上の積分の定義は以下のイメージです.
非負単関数は有限個の段差を持つ見た目をしているとみなせます.
上の定義は,「この関数の積分は各四角形の面積を足し合わせたもの」と定めていると解釈できます.
ただし,各四角形の面積を横幅を測度 \(\mu\) による値,高さを \(h\) の値として計算しています.
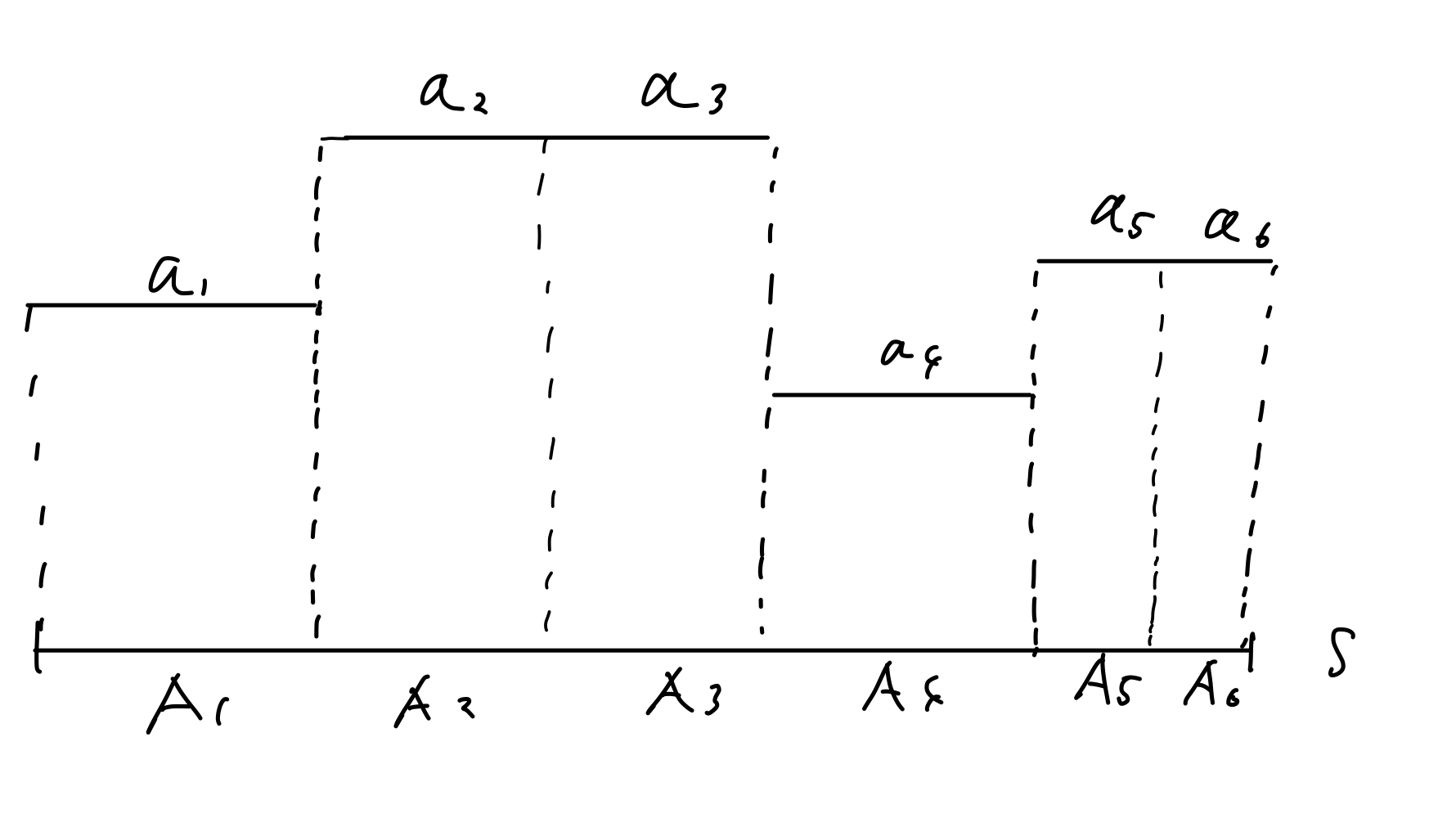
また,「well-definedである」とは次のことを意味します.
非負単関数 \(h\) の表示の仕方は一意ではありません.例えば,上の図のように \(h\) が表示されているとしたとき,別の表示として,\(A_2, A_4\) をそれぞれ2つの可測集合にさらに分割して添字を振り直した以下の図の表示も \(h\) の表示です.
定義中の「well-definedである」とは,「どんな表示の仕方をしても積分値 \(\int_S h d\mu\) は変わらない」ということを意味しています.
本当に変わらないか,測度の加法性を使ってチェックしてみると良い練習になるかなと思います.
非負可測関数の積分
非負単関数の積分を用いて,非負可測関数の積分を定義します.
定義2. (非負可測関数の積分)\( f \in \mathbb{M}(S \to [0, \infty)), A \in \mathscr{A} \) とする. \(f \) の測度 \(\mu\) による \(A\) 上の積分を以下で定義する: \(\int_A f d\mu := \sup \left \{ \int_A h d\mu \mid h \in \mathbb{S}(S \to [0, \infty))\ \text{s.t.}\ h \leq f \ \text{on}\ A \right \} \), ここで,\( h \leq f \ \text{on}\ A \stackrel{\text{def}}{\Leftrightarrow} h(x) \leq f(x) \ \text{for}\ \forall x \in A \).
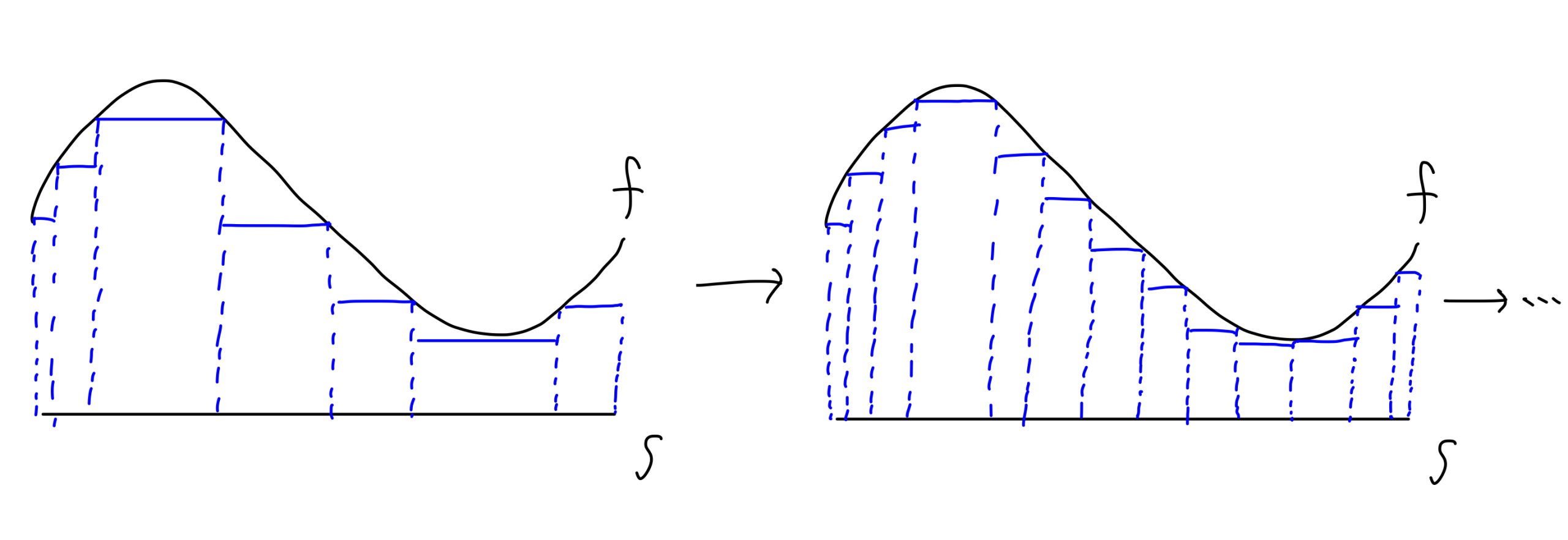
定義2のイメージは以下です.
非負可測関数を下から非負単関数で近似して,その非負単関数の積分値の上限をその非負可測関数の積分値と定めています.
やっていることのイメージはリーマン積分と似ていると感じるかもしれませんが,リーマン積分と違うのは近似する四角形の面積の計算の際に横幅を測度 \(\mu\) で与えている点です.
また,リーマン積分では,最初に\(S\) を小区間(i.e. 横)に分割してから縦(i.e. 小区間におけるある点での \(f\) の値)を使って四角形の面積を計算していましたが,測度を用いた積分では \(f\) の値域を小区間に分割してから,\(S\) をその小区間の引き戻しで表される可測集合に分割しているという違いがあるともみなせます(cf. 非負可測関数の非負単関数による下からの近似列の構成).
可測関数の積分
非負とは限らない,一般の実数値可測関数に対して積分を定義します.
定義3. (実数値可測関数の積分) \( f \in \mathbb{M}(S \to \mathbb{R}) , A \in \mathscr{A}\) とする. \(\int_A f^+ d\mu\ \text{or}\ \int_A f^- d\mu \lt \infty \) であるとき,\(f\) は \(A\) 上積分確定といい,\(f\) の\(A\) 上での積分を以下で定義する: \( \int_A f d \mu := \int_A f^+ d\mu \ - \int_A f^- d\mu \), ここで,\(f^\pm := \max\{\pm f, 0\}\).
また,\(\int_A |f| d\mu \lt \infty \) であるとき,\(f\) は \(A\) 上可積分であるという.
まず,前回の記事の命題15から,\( f^\pm \in \mathbb{M}(S \to [0, \infty)) \) であるため \(f^\pm\) に対しては定義2から積分が定義できていることに注意してください.
また,\(|f| = f^+ + f^-\) と書けるので,\(|f|\) の積分は非負可測関数の積分であるため既に定義できていることに注意してください.
そして,定義3で行っていることは,\(f\) を positive part と negative part に分けて,それぞれに対して積分値を計算してその差で \(f\) の積分を定義していることになります.
「積分確定」という条件を考えていますが,例えば積分確定でない \(f \in \mathbb{M}(S \to \mathbb{R})\) の例として以下が挙げられます:
\( (S, \mathscr{A}, \mu) \) として \((\mathbb{R}, \mathscr{B}(\mathbb{R}), \mathscr{L})\) を考え,\(f\) として \(f(x) = \begin{cases} 1 & (x \geq 0) \\ 0 & (x \lt 0) \end{cases} \) を考えます.
ここで,この記事と前回の記事で未定義ですが,\( \mathscr{L}\) はルベーグ測度を表します.
詳しい説明は省略しますが,ここでの大事な性質として \(\mathscr{L}([0, \infty)) = \infty, \mathscr{L}((-\infty, 0)) = \infty\) が成り立ちます.
これにより,\(\int_S f^+ d\mu = \infty, \int_S f^- d\mu = \infty \) となるので,上の \(f\) は積分確定でないことが分かります.
ほとんど至る所
積分の性質を述べる前に,測度論における重要な概念である以下を定義します.
定義4.(ほとんど至る所)\(A \in \mathscr{A}\) とし,\(x \in A\) についての命題\(P(x)\) を考える. \( B := \left\{ x \in A \mid P(x)\ \text{が定義され}, P(x)\ \text{が真} \right\} \) に対し,以下が成り立つとき,命題 \(P(x)\) は \(\mu\) について \(A\) 上ほとんど至る所成り立つといい,「\(P, \mu\text{-a.e. on }A\)」と記述する: \( \exists N \in \mathscr{A}\ \text{s.t.}\ A\setminus B \subset N, \mu(N) = 0\).
上の定義は,測度0の点を除いて命題 \(P(x)\) が成り立っていることを意味しています.
お気持ちとしては,測度0なら無視しちゃおうという感じです.
例えば,「\(f \leq g, \mu\text{-a.e. on A}\)」は「ある測度0の集合に含まれる集合を除いて,\(A\) 上で \( f\leq g\) が成り立っている」ことを意味します.
言い換えると,\(\{ x \in A \mid f(x) \gt g(x) \}\) この集合が測度0の集合に含まれている事を意味しています.
積分の性質と積分と極限の交換可能性
ここでは,積分の性質と積分と極限の順序交換に関する幾つかの命題を紹介します.
命題5.(積分に関する性質)\( f, g \in \mathbb{M}(S \to \mathbb{R}) , a, b \in \mathbb{R}, A \in \mathscr{A}\) とし,\(f, g\) は \(A\) 上積分確定とする. このとき,以下が成り立つ: (i) \(\mu(A) = 0 \Rightarrow \int_A |f| d\mu = 0 \), (ii) \( \int_A f d\mu = \int_S f 1_A d\mu \), (iii) \( f \leq g\ \mu \text{-a.e. on } A \Rightarrow \int_A f d\mu \leq \int_A g d\mu \). また, \( \int_A f^+ d\mu + \int_A g^+ d\mu \lt \infty\) or \(\int_A f^- d\mu + \int_A g^- d\mu \lt \infty \) が成り立つとき,以下が成り立つ: (iv) \(\int_A (af + bg) d\mu = a \int_A f d\mu + b \int_A g d\mu\) (線形性). 特に,以下が成り立つ: (v) \( \left | \int_A f d\mu \right | \leq \int_A |f| d\mu \).
proof 例えば,「ルベーグ積分入門 --使うための理論と演習」参照.
次に極限に関する命題を紹介します.
命題6. (種々の収束定理)\( \{f_n\}_{n\geq 1} \subset \mathbb{M}(S \to \mathbb{R}) , g \in \mathbb{M}(S \to [0, \infty)), A \in \mathscr{A}\) とし,\( \int_A g d\mu < \infty\) とする. (i) 単調収束定理 \(f_1 \geq -g\) かつ \(f_n \nearrow f \Rightarrow \lim_{n \to \infty} \int_A f_n d\mu = \int_A f d\mu\).
(ii) 優収束定理 \( \lim_{n\to \infty} f(x) = f(x), \sup_{n\geq 1}|f_n(x)| \leq g(x) \ \text{for}\ \forall x \in A\) \( \Rightarrow \lim_{n\to\infty} \int_A |f - f_n| d\mu = 0\). 従って,\(\lim_{n\to\infty} \int_A f_n d\mu = \int_A f d\mu \)
(iii) Fatouの補題 (iii-1) \( -g(x) \leq \inf_{n\geq1}f_n(x) \ \text{for}\ \forall x \in A\) \(\Rightarrow \int_A \liminf_{n\to\infty} f_n d\mu \leq \liminf_{n\to\infty} \int_A f_n d\mu\) (iii-1) \( \sup_{n\geq1}f_n(x) \leq g(x) \ \text{for}\ \forall x \in A\) \(\Rightarrow \limsup_{n\to\infty} \int_A f_n d\mu \leq \int_A \limsup_{n\to\infty} f_n d\mu\)
proof 例えば,「ルベーグ積分入門 --使うための理論と演習」参照.
命題7.(押し出し測度による積分)\((S_1, \mathscr{A}_1, \mu)\): 測度空間,\((S_2, \mathscr{A}_2)\): 可測空間,\(\varphi: S_1 \to S_2\) : \(\mathscr{A}_1/\mathscr{A}_2\)-可測写像, \(\mu_\varphi\): \(\varphi\) による \(\mu\) の押し出し測度, \(A \in \mathscr{A}_2, f \in \mathbb{M}(S_2 \to \mathbb{R})\): \(A\) 上積分確定(\(\mu_\varphi\)に対して)とする. このとき,以下が成り立つ: \( \int_A f d\mu_\varphi = \int_{\varphi^{-1}(A)} f \circ \varphi d\mu \).
proof \(f^\pm\) に分解し,\( \{f^\pm_n\}_{n\geq1} \subset \mathbb{S}(S \to [0, \infty))\ \text{s.t.}\ f^\pm_n \nearrow f^\pm \) を取ると \( f_n^\pm \circ \varphi \nearrow f^\pm \circ \varphi\) なので,各 \(f^\pm_n\) に対し \( \int_A f_n^\pm d\mu_\varphi = \int_A f_n \circ \varphi d\mu \) を示し,単調収束定理を用いれば良い.\( \int_A f_n^\pm d\mu_\varphi = \int_A f_n \circ \varphi d\mu \) は \(\int_S 1_A d\mu = \mu(A) \) に注意すれば検証できる.
命題5は積分に関する基本的な性質を述べています.
例えば,リーマン積分は線形性が成り立ちますが,測度による積分でも線形性が成り立つことを主張しています.
命題6は積分と極限の順序交換についての主張です.
これ単体だと嬉しさが伝わりづらいのですが,測度論を用いていると積分と極限の順序交換ができると嬉しい場面が多々ありまして,そのようなケースで重宝する主張です.
例えば,舟木先生著「確率論」において,中心極限定理の証明で優収束定理が用いられています.
また,積分と微分の順序交換について議論する際にも優収束定理が使われます.
命題7は押し出し測度と積分の関係性についての主張です.
確率変数の分布が押し出し測度であった(cf. 前回の記事の「押し出し測度」の章)ので,この命題を用いれば,期待値の積分の意味がより具体的に分かります.
例えば,\( (\Omega, \Sigma, P) \): 確率測度空間,\((S, \mathscr{A})\): 可測空間, \( X: \Omega \to S\): \(\Sigma/\mathscr{A}\)-可測関数(S-値確率変数)としたとき,\(S\) 上の \(\mathscr{A}/\mathscr{B}(\mathbb{R})\)-可測関数 \(f: S \to \mathbb{R}\) の期待値は,押し出し測度 \(P_X\) を用いて以下の形で表されます:
\( \mathbb{E}[f] = \int_S f dP_X = \int_\Omega f\circ X dP \).
前回の記事の最初にお話しした,期待値の測度による積分としての表示が得られたわけです.
終わりに
本記事では前回の続きとして,測度を用いた可測関数の積分の定義および積分の種々の性質と極限と積分の順序交換可能性について紹介しました.
これでadvent calendarでの測度論のトピックの紹介は終了になります.
しかしながら,今回と前回で紹介できたトピックは測度論の中のほんの一部の話題になります.
もし,他のトピックも知りたい方がいらっしゃいましたら,例えば,以下の文献を参考文献として挙げさせてもらいます:
- 新装版 ルベーグ積分入門 --使うための理論と演習,吉田伸生先生著
本記事を読んで測度論に興味を持つ方がいてくださったり,測度論の雰囲気が伝わっていましたら幸いです.
明日はAIチームの友松から"2022年のTech Blogと対外発表の振り返り"についての記事が出る予定です.
そちらも合わせてご覧いただけますと幸いです.






