こんにちは
AIチームの戸田です
今回はTransformerモデルにMonte Carlo(MC) Dropoutを適用して、その効果を検証してみたいと思います
MC Dropout
MC Dropoutはニューラルネットにおいて、学習時のみでなく推論時にもDropoutを使うことで、近似的にベイズ推論を行う手法です。提案された論文はこちらになります。
ニューラルネットワークはよくブラックボックスだと言われており、どうしてその予測結果になったのかを推定することは困難です。MC DropoutはDropoutを使って学習したニューラルネットワークに対して、推論時の追加実装のみでモデルが予測に対してどれだけ自信をもっているかの確信度(のようなもの)を得ることができます。
詳細は元論文を読んでいただきたいのですが、ざっくり概要をまとめると以下のようになります
- ニューラルネットワークの重みを一定値ではなく分布とみなす
- Dropoutは各重みのパスをランダムに切るので、推論時に使うことでニューラルネットの重みの分布からサンプリングをしていることになる
- これを複数回繰り返すことで、予測値の分布を近似的に求めることができる
- 予測値の分布の裾の広がりを見ることで,予測に対する確信度(のようなもの)を評価できる
追加の実装はほぼ必要なく、既存のコードへの組み込みもやりやすい手法だと思います。
Transformerモデルへの適用
このMC Dropout、元論文ではLeNetや5層のfeed forward neural networkといった比較的シンプルなニューラルネットワークに適用されていたのですが、近年NLPで主流となっているTransformerに適用した場合の効果を検証してみたいと思います。
データセット
scikit-learnのfetch_20newsgroupsを使います。こちらは18846件のニュース記事をスポーツや政治などの20種類のカテゴリに分類するタスクになります。
以下のようにしてデータを読み込みます。
from sklearn.datasets import fetch_20newsgroups
datasets = fetch_20newsgroups()
texts = datasets['data']
targets = datasets['target']
n_classes = len(datasets['target_names'])StratifiedKFoldを使ってデータを学習用と評価用に分割します。
kf = StratifiedKFold(n_splits=5, shuffle=True, random_state=0)
for fold, (train_idx, valid_idx) in enumerate(kf.split(X=texts, y=targets)):
train_texts = list(np.array(texts)[train_idx])
valid_texts = list(np.array(texts)[valid_idx])
train_targets = targets[train_idx]
valid_targets = targets[valid_idx]
break # only one foldPytorchを使って学習を行いたいのでDatasetクラスを定義します
from torch.utils.data import Dataset, DataLoader
class News20Dataset(Dataset):
def __init__(self, texts, targets):
self.texts = texts
self.targets = targets
def __len__(self):
return len(self.texts)
def __getitem__(self, item):
tok = GCF.TOKENIZER(self.texts[item], max_length=GCF.MAX_LEN, truncation=True, padding='max_length',)
return {
'input_ids': torch.tensor(tok['input_ids'], dtype=torch.long),
'attention_mask': torch.tensor(tok['attention_mask'], dtype=torch.long),
'target': torch.tensor(self.targets[item], dtype=torch.long)
}GCF(glocal config)はこの後定義します。こちらのDatasetクラスにStratifiedKFoldで分割したテキストとラベルデータを代入してDataLoaderまで定義してしまいましょう。
train_dset = News20Dataset(train_texts), train_targets)
valid_dset = News20Dataset(valid_texts), valid_targets)
train_dloader = DataLoader(train_dset, batch_size=GCF.BS,
pin_memory=True, shuffle=True, drop_last=True)
valid_dloader = DataLoader(valid_dset, batch_size=GCF.BS,
pin_memory=True, shuffle=False, drop_last=False)これでデータセットの準備は完了です。
モデリング
まずはGCFを定義します。
from transformers import AutoTokenizer, AutoConfig
class GCF:
MODEL_NAME = 'distilbert-base-uncased'
TOKENIZER = AutoTokenizer.from_pretrained(MODEL_NAME,normalization=True)
CONFIG = AutoConfig.from_pretrained(MODEL_NAME)
N_EPOCHS = 3
BS = 64
MAX_LEN = 256
LR = 3e-5
WEIGHT_DECAY = 1e-4パラメータは決め打ちで、モデルは計算リソースの都合によりDistilBERTを使います。この設定で以下のようなモデルを定義します。
import torch.nn as nn
from transformers import AutoModel
class News20Model(nn.Module):
def __init__(self):
super(News20Model, self).__init__()
GCF.CONFIG.dropout = 0.5
GCF.CONFIG.output_hidden_states=True
self.transformer = AutoModel.from_pretrained(
GCF.MODEL_NAME,
config=GCF.CONFIG,
)
self.classifier = nn.Linear(GCF.CONFIG.hidden_size, n_classes)
def forward(self, input_ids, attention_mask, target=None):
outputs = self.transformer(
input_ids,
attention_mask=attention_mask,
)
h = outputs['last_hidden_state'][:, 0, :]
h = self.classifier(h)
if target is not None:
loss = nn.CrossEntropyLoss()(h, target)
else:
loss = None
return loss, hデフォルトの設定からの変更点として、TransformerのDropout率を0.5にしています。理由としては、元論文において分類問題のMNISTの検証を行う際にDropout率を0.5に設定しているからで、特に手元で調整したわけではありません。ちなみに回帰問題のCO2データセットでは0.1~0.2を設定していたので、問題設定やモデルによって調整が必要なのかもしれません(このあたり、まだちゃんと理解できていないです・・・)
学習
上記で定義したモデルを使って学習を行います。
from tqdm.auto import tqdm
import torch
from transformers import AdamW
device = torch.device("cuda")
model = News20Model()
model.to(device)
optimizer = AdamW(model.parameters(), lr=GCF.LR, weight_decay=GCF.WEIGHT_DECAY)
losses = []
for epoch in range(GCF.N_EPOCHS):
print(f"epoch {epoch}")
model.train()
for d in tqdm(train_dloader, total=len(train_dloader)):
loss, _ = model(
d['input_ids'].to(device),
d['attention_mask'].to(device),
d['target'].to(device)
)
optimizer.zero_grad()
loss.backward()
optimizer.step()
losses.append(loss.item())
学習lossを以下のコードでプロットしてみます。
import seaborn as sns
from matplotlib import pyplot as plt
sns.set()
sns.set_style('whitegrid')
sns.set_palette('Set3')
plt.plot(losses);
plt.show()
モデルの精度を以下のコードで評価すると、正解率は約83.8%となりました
predicts = []
model.eval()
for d in tqdm(valid_dloader, total=len(valid_dloader)):
with torch.no_grad():
_, pred = model(
d['input_ids'].to(device),
d['attention_mask'].to(device),
d['target'].to(device)
)
predicts.append(pred.cpu())
predicts = torch.vstack(predicts)
acc = (targets[valid_idx] == predicts.argmax(1).numpy()).mean()
# acc -> 0.8382677861246134予測の確信度
MC Dropoutで予測の確信度を得ます。上記推論コードに少し改良を加えて、DropoutをONにした状態で同じデータに対して100回推論を行います。
predicts = []
model.train() # Dropout ON
for d in tqdm(valid_dloader, total=len(valid_dloader)):
with torch.no_grad():
_preds = []
for _ in range(100):
_, pred = model(
d['input_ids'].to(device),
d['attention_mask'].to(device),
d['target'].to(device)
)
_preds.append(pred.cpu())
predicts.append(torch.stack(_preds))
predicts = torch.cat(predicts, 1)この100回の予測の内の最頻値をモデルの予測とし、最頻値の出現率をモデルの確信度とします。
res = []
for idx, label in enumerate(targets[valid_idx]):
pred = predicts[:, idx, :].argmax(1).numpy()
pred_y, count = scipy.stats.mode(pred)
trust = count[0] / 100
res.append({
'y_true': label,
'y_pred': pred_y[0],
'trust': trust
})
result_df = pd.DataFrame(res)このように計算した確信度を正解したものと不正解だったものに分けて箱ひげ図にしてみると以下のようになります
df1 = result_df.query("y_true == y_pred")[['trust']]
df1['ansewer'] = 'correct'
df2 = result_df.query("y_true != y_pred")[['trust']]
df2['ansewer'] = 'failed'
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
sns.boxplot(x='ansewer', y='trust', data=pd.concat([df1, df2]), showfliers=False, ax=ax)
plt.show()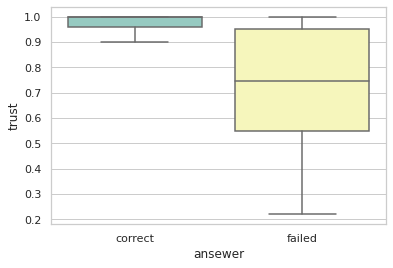
正解データ(correct)は確信度(trust)が高く、不正解データ(failed)は確信度が低そうに見えます。
Transformerのような複雑なモデルでもMC Dropoutで確信度を測ることができることがわかりました。
おわりに
本記事ではTransformerモデルにMC Dropoutを適用した際の効果について検証してみました。
結果、Transformerモデルでもモデルの確信度を得ることができました。今回は分類問題で検証しましたが、回帰問題でも予測の分散などを利用することで確信度を得ることができるようです。加えて、回帰問題ではDropoutは悪影響を及ぼすことがありますが、MC Dropoutで、複数回予測した平均をとるとこの悪影響を緩和できる、といった実験結果(link)もあるようです。手軽に試せる手法なので、積極的に利用していきたいですね。
余談になるのですが、以前産学連携における音声分類タスクでこのMC Dropoutが絶大な効果を発揮し、何か他のモデル/タスクにも応用できないかと考えたのが本記事を書くきっかけでした。ベイズ推論に関しては全くの素人なのですが、また時間をとって勉強してみたいと思います。
最後までお読みいただきありがとうございました!






