こんにちは.AIチームの邊土名です.
本記事は AI Shift Advent Calendar 2021 の16日目の記事です.
以前投稿した記事では,最適輸送に基づいたテキスト間類似度計算手法を用いてEntity Linkingの評価実験を行いました.
本記事では,最適輸送における単語の重み(重要度)に焦点を当て,再度Entity Linkingの実験を行っていこうと思います.
はじめに:最適輸送における単語の重み
最適輸送に基づくテキスト間の類似度計算に用いられる Earth Mover's Distance (EMD) は,ある確率分布\(\mu\)からもう片方の確率分布\(\mu^{\prime}\)へと荷物を輸送する際の最小コストと定義されています.このとき,EMDの入力は以下の図のようになります.

このEMDを用いてテキスト間の類似度(距離)を計算する場合,2つのテキスト\(s=\{t_1, t_2, \cdots, t_i, \cdots, t_n\}, s^{\prime}=\{t^{\prime}_1, t^{\prime}_2, \cdots, t^{\prime}_j, \cdots, t^{\prime}_{n^{\prime}}\}\)は確率分布\(\mu, \mu^{\prime}\)に,単語\(t_i, t^{\prime}_j\)(または単語ベクトル\(w_i, w^{\prime}_j\))は点\(x_i, x^{\prime}_j\)に対応します.
そして,単語\(t_i, t^{\prime}_j\)の重み(重要度)は,各点の荷物の量を表す確率質量\(m_i,m^{\prime}_j\)に対応します.
最適輸送においては,確率質量が大きい,すなわち重要度の高い単語ほど適切にアライメントされやすくなる(=適切に輸送しないと輸送コストが増大する)ため,単語重要度を考慮することでより高精度にテキスト間類似度を測れるようになることが期待できます.
そこで,今回の実験では,単語の重み付け方法の違いによってどの程度Entity Linkingの性能に差がでるのかを検証してみました.
実験
実験に用いるデータセットや比較手法等は以前行ったEntity Linking実験と同じですので,詳細についてはこちらの記事をご覧ください.
単語の重み付け方法
今回の実験では4種類の単語重み付け方法を採用しました.
一様重み (Uniform)
Word Mover's Distance (WMD)[Kusner+, ICML2015] では,全ての単語に一様な重みが付与されています.
すなわち,2つのテキスト\(s, s'\)の確率分布\(\mu_{s}, \mu_{s^{\prime}}\)は次のように定義されます.
\begin{equation}
\mu_{s} = \left\{\left(w_i, \frac{1}{n}\right)\right\}^n_{i=1} \\
\mu_{s^{\prime}} = \left\{\left(w^{\prime}_{j}, \frac{1}{n^{\prime}}\right)\right\}^{n^{\prime}}_{j=1}
\end{equation}
単語ベクトルのノルム (Norm)
Word Rotator’s Distance (WRD)[Yokoi+, EMNLP2020]では,単語ベクトルのノルム(長さ)には単語の重要度がエンコードされているとして,各単語ベクトル\(w_i\)のノルム\(\lambda_i=||w_i||\)を単語の重みとして利用しています.
このとき,2つのテキスト\(s, s'\)の確率分布\(\mu_{s}, \mu_{s^{\prime}}\)は次のように定義されます.
\begin{equation}
\mu_{s} = \left\{\left(w_i, \frac{\lambda_i}{Z}\right)\right\}^n_{i=1} \\
\mu_{s^{\prime}} = \left\{\left(w^{\prime}_{j}, \frac{\lambda_j}{Z^{\prime}}\right)\right\}^{n^{\prime}}_{j=1}
\end{equation}
ここで,\(Z, Z^{\prime}\)は正規化定数です.
Inverse Document Frequency (IDF)
あるEntity辞書において,どのエントリにも含まれているような単語は,エントリの識別という観点では有用ではありません.
たとえば,医療系ドメインのEntity辞書では「○○病院」といったエントリが多数登録されているため,単語「病院」の重要度は低くしたいという気持ちがあります.
そこで,Entity辞書内に存在する各エントリをひとつの文書と見なして各単語のIDFスコアを計算し,そのIDFスコアを確率質量として用いてみることにしました.
2つのテキスト\(s, s'\)の確率分布\(\mu_{s}, \mu_{s^{\prime}}\)は次のように定義されます.
\begin{equation}
\mu_{s} = \left\{\left(w_i, \frac{\mathrm{IDF}(t_i)}{Z}\right)\right\}^n_{i=1} \\
\mu_{s^{\prime}} = \left\{\left(w^{\prime}_{j}, \frac{\mathrm{IDF}(t^{\prime}_j)}{Z^{\prime}}\right)\right\}^{n^{\prime}}_{j=1}
\end{equation}
Phonetic Soft IDF (PS-IDF)
先ほどIDFを考慮すると良さそうだ,という話をしましたが,ここで問題となってくるのが音声認識誤りです.
音声認識誤りが生じた場合,IDFスコアのルックアップテーブルを正しく参照することができなくなるため,適切な単語の重み付けができなくなってしまいます.
そこで, 新たな単語重み付け手法 Phonetic Soft IDF (PS-IDF) を作成しました.
PS-IDFは Soft TFIDF[Cohen+, IIWEB2003]という手法を参考に作成しました.
Soft TFIDF は,TFIDFスコアを求めたい単語と類似する単語集合を取得し,それらの単語との類似度を重みとしたTFIDFスコアの加重平均を計算することでTFIDFスコアを求める手法です.
これにより,ルックアップテーブルに存在しない単語であってもTFIDFスコアを算出することができます.
PS-IDFは,単語の音素列の類似度を考慮して``Soft"にIDFスコアを計算する手法です.式で表すと以下のようになります.
\begin{equation}
\mathrm{PSIDF}(t_i) = \frac{1}{|\mathcal{D}(p_i,P^e, \theta)|} \sum_{p^e_j \in \mathcal{D}(p_i,P^e,\theta)}\mathrm{IDF}(p^e_j) \cdot (1 - d_\mathrm{edit}(p_i, p^e_j))
\end{equation}
ここで,\(p^e_j\)はEntity辞書内にあるエントリの構成単語\(t^e_j\)の音素列,\(P^e\)はEntity辞書内にあるエントリの単語音素列の集合です.
また,\(\mathcal{D}(p_i,P^e,\theta)\)は,\(P^e\)に含まれる単語音素列\(p^e_j\)のうち,音素列\(p_i\)との正規化レーベンシュタイン距離が\(d_\mathrm{edit}(p_i, p^e_j) \leq \theta\)であるものの集合であり,\(\theta\)はしきい値(ハイパーパラメータ)となっています.
今回の実験では,\(\theta=0.2\)に設定しています.
最終的に,2つのテキスト\(s, s'\)の確率分布\(\mu_{s}, \mu_{s^{\prime}}\)は次のように定義されます.
\begin{equation}
\mu_{s} = \left\{\left(w_i, \frac{\mathrm{PS IDF}(t_i)}{Z}\right)\right\}^n_{i=1} \\
\mu_{s^{\prime}} = \left\{\left(w^{\prime}_{j}, \frac{\mathrm{PS IDF}(t^{\prime}_j)}{Z^{\prime}}\right)\right\}^{n^{\prime}}_{j=1}
\end{equation}
Entity辞書内実験
はじめに,Entity 辞書に登録された同義語を入力として与え,その同義語に対応するエントリとを紐付ける Entity 辞書内実験を行いました.
評価結果を以下の表に示します.
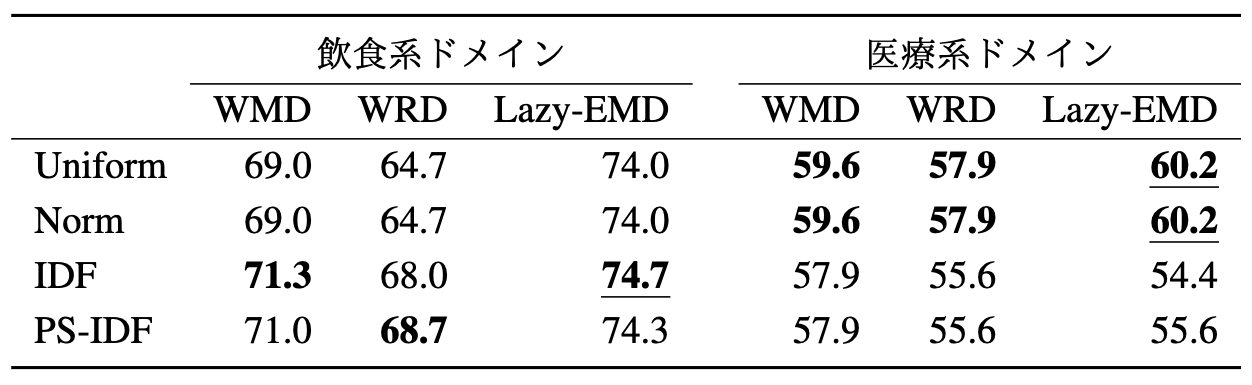
結果をみると,一様な重み付けをした際のスコアと単語ベクトルのノルムで重み付けした際のスコアが一致しています.
Entity辞書内のエントリの単語は,基本的に名詞かつ意味的にも類似した単語で占められているため単語間のノルムの大きさにさほど差が出ず,結果として一様な重み付けと同じスコアになったものと考えられます.
ドメインごとに結果を見ていくと,飲食系ドメインでは単語の重みにIDF,PS-IDFを用いた手法のAccuracyが高い結果となりました.
一方,医療系ドメインでは,一様重みやノルム重みの方が良い結果を示しています.
医療系ドメインのEntity辞書には音声認識誤りフレーズが多く登録されているため,IDF系の手法では適切な単語の重みが求めにくく,結果として性能が低くなってしまったと考えられます.
発話ログデータを用いた実験
次に,発話ログデータを用いて,実際のユーザ発話が与えられた際の Entity Linking の性能を評価しました.評価結果を以下の表に示します.
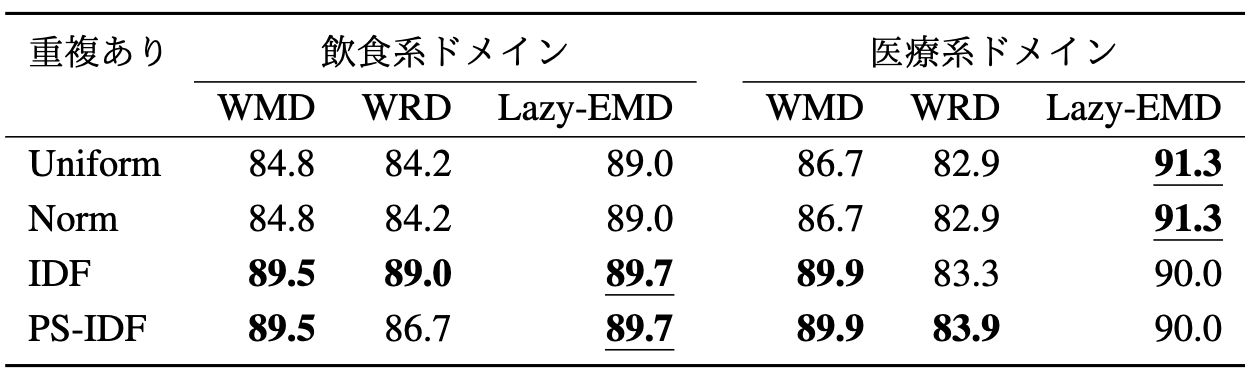
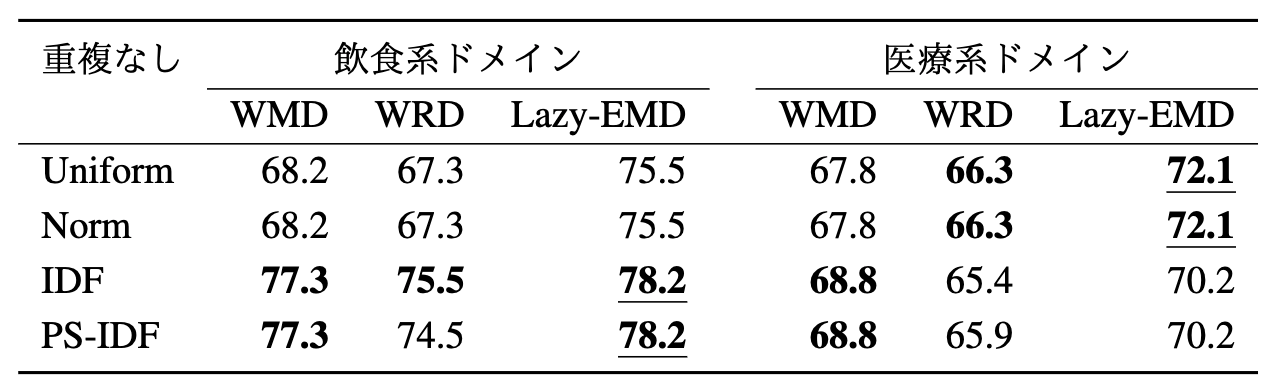
ドメインごとに結果を見ていくと,飲食系ドメインでは単語の重みにIDF,PS-IDFを用いた手法のAccuracyが高い結果となりました.
一方,医療系ドメインでは,一様重み,ノルム重みを用いたLazy-EMDが最も高い性能を示しています.なお,IDF系の重み付けを適用した際のスコアが最良となっている箇所もあることから,IDF系の重み付けもある程度効果があると思われます.
おわりに
今回の記事では,最適輸送における単語の重み(重要度)に焦点を当て,単語の重み付け方法の違いによってどの程度Entity Linkingの性能に差がでるのかを検証してみました.
IDF系の単語重み付けですが,飲食系ドメインの結果を見る限り音声認識誤りをもう少しうまく考慮できるようになると,かなり良い感じに性能が向上するような気がしています.音韻特徴をうまく取り入れた手法の検討を進めていきたいところです.
最後までお読みいただきありがとうございました!
明日は開発チームの滝波の記事が公開される予定ですので,是非そちらもご覧ください!






