はじめに
こんにちは,AIチームの下山です.
本記事は AI Shift Advent Calendar 2022 の20日目の記事です.
本記事と24日目の記事の2つで,可測空間・測度空間の定義から始めて測度による積分を最短(と個人的に思っている)で紹介しようと思います.
本記事では,事前準備として,可測空間・測度空間の定義からはじめ,可測写像の定義と可測写像に対して成り立ついくつかの性質を紹介します.
記事のスタイルとして,定義・命題とお気持ちを分離したいので,はじめに定義・命題を述べ,次にお気持ちを記述する流れで記載しようと思います.
簡単な命題については証明を与えようと思いますが,証明は基本的には別の本にお任せする形にします.
以下にこのような記事を執筆しようと思った理由を記載します.
最近,業務で確率論の知識があると理解が深まって嬉しい場面に何回か遭遇し,(さわりだけですが)舟木先生著「確率論」で勉強しました.
その際に,測度論の知識として,可測写像の積分について知っておくと期待値をはっきりと理解できるなと感じました.
しかし,測度論を勉強したことがない方が1から測度による積分までを勉強しようとすると,そこに到達するまでにもいくつもの話題があるため,少しハードルが高いと感じる方もいるかもしれないと考えました.
そこで,測度による積分までを最短で導入し,積分を定義するまでにどんな概念が必要かをざっくりと俯瞰できる記事を書いてみようかなと考えました.
本記事の内容が測度論に興味を持っている方・勉強している方の役に立てたなら嬉しいです.
本文
可測集合と測度
まず,可測集合と測度を定義します.
定義1.(\(\sigma\)-加法族と可測空間) \(S\): 集合 とする.
\(\mathscr{A} \subset 2^S \) が以下の条件を満たすとき,\(\mathscr{A}\)は\(\sigma \)-加法族であると言う:
(i) \( \emptyset \in \mathscr{A} \)
(ii) For \( \forall A \in \mathscr{A} \), \(A^c \in \mathscr{A}\)
(iii) For \(\forall \{A_n\}_{n\geq1} \subset \mathscr{A}, \bigcup_{n\geq1}A_n \in \mathscr{A} \)
また,\( \sigma\)-加法族 \(\mathscr{A} \subset 2^S\) に対し,\( (S, \mathscr{A}) \)を可測空間と呼び,\( \mathscr{A} \) の元を可測集合と呼ぶ.
定義1の(ii)と(iii)を組み合わせると以下の命題が成り立ちます.
命題2. \((S, \mathscr{A}) \): 可測空間とする. このとき,以下が成り立つ: For \(\forall \{A_n\}_{n\geq1} \subset \mathscr{A}, \bigcap_{n\geq1}A_n \in \mathscr{A} \)
定義3.(測度) \((S, \mathscr{A}) \): 可測空間とする. 関数 \(\mu : \mathscr{A} \to [0, \infty] \) が以下の条件を満たすとき,\(\mu\) を測度と呼び,\((S, \mathscr{A}, \mu) \) を測度空間と呼ぶ: (i) \( \mu(\emptyset) = 0 \) (ii) \( \{A_n\}_{n\geq0} \subset \mathscr{A}, A_0 = \sum_{n \geq 1} A_n \Rightarrow \mu(A_0) = \sum_{n \geq 1} \mu(A_n)\) ここで,\(A_0 = \sum_{n \geq 1} A_n\)は「\(A_0 = \bigcup_{n\geq1} A_n\) かつ \(i\neq j \Rightarrow A_i \cap A_j = \emptyset,\ \text{for}\ \forall i, \forall j \geq 1 \)」を意味する.
それでは,お気持ち(これは私なりの解釈です)を説明します.
測度と可測空間はセットで考えてあげると分かりやすいかなと思います.
測度は集合族(要素が集合である集合)の上で定義される非負関数です.
つまり,集合を1つ食べると,何か非負の数を1つ吐き出す写像です.
これは,集合\(A\in\mathscr{A}\)に対して大きさ\(\mu(A)\)を割り当てているとみなせます.
ここで,注意してほしいのが,定義域に含まれていない集合には値を割り当てられる保証がないと言う点です.(\(A \notin \mathscr{A}\)なら,\(\mu(A)\)は一般には定まりません.)
測度の定義においては,測度が食べることができる集合をあらかじめ全て列挙していると言うことになります(それが\( \sigma\)-加法族です.)
もう少し,測度について掘り下げます.
測度は面積概念の一般化と考えることができます.
例えば,四角形に対してその面積を考えると,それは四角形と言う集合に面積と言う非負の値を割り当てている写像だとみなせます.
このイメージを踏まえて性質(i)と(ii)を見ていきます.
測度の性質(i)は空集合は大きさが0であってねという制約になります.
四角形で置き換えると,空の四角形の面積は0だよねと言っています.
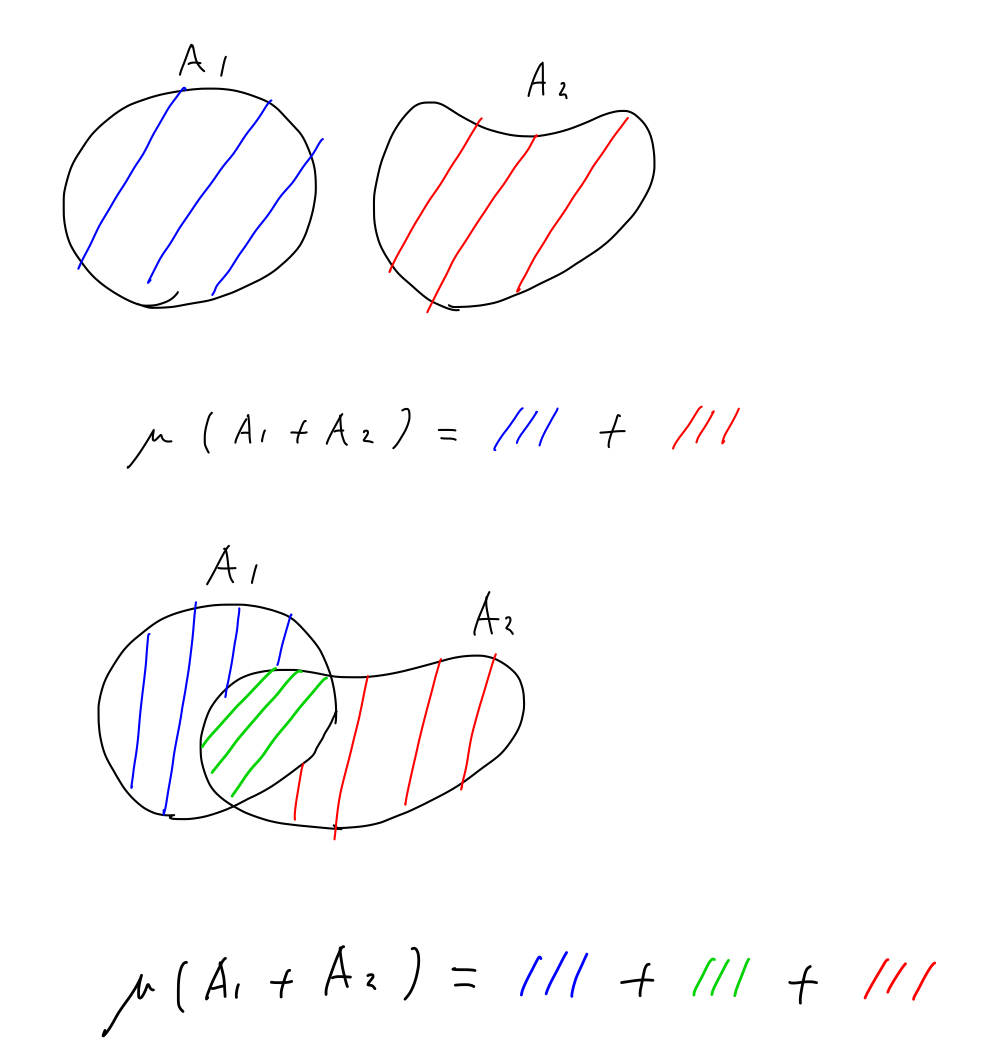
性質(ii)は「重なっていない集合全体の大きさは,各集合の大きさの和になるよ」と言うことを意味しています.
イメージとしては,以下の図のように,集合を重なっていない部分に分割した時に,その集合の大きさ(測度)は重なっていない部分の測度の和になります.
そして,性質(ii)の最大のポイントが加算回の操作を許容している点です.
(本記事では触れられないかもしれませんが,この「加算回の操作を許す」という点から直感に反する非自明な結果が多々導かれます.)
次に\(\sigma\)-加法族の定義のお気持ちを説明します.
上で述べたように,\(\sigma\)-加法族は測度が食べられる集合全体を規定したものでした.
そして,測度の定義には,「加算回の集合演算によって得られた集合もまた食べることができてほしい」と言うお気持ちがありました.
つまり,\(\sigma\)-加法族はその中に含まれる集合に対し加算回の操作をした集合を含んでほしいことになります.
実は,定義1.(i)~(iii)および命題2から,\(\sigma\)-加法族は加算回の集合演算(補集合,共通部分,和集合)に関して閉じていることが分かります.
これは,「測度が食べられる集合を加算個持ってきたときに,それらの集合に対して加算回の集合演算で得られる集合もまた測度が食べることができてね」と言う要請をバッチリ満たしていることが分かります.
\(\sigma\)-加法族はそれ単体で定義を見てもお気持ちが見えづらいかと思いますが,測度とセットで考えてあげると多少分かりやすくなるのではないかなと思います.
ある集合族を含む最小の\(\sigma\)-加法族とボレル集合族
一般に,集合族 \(\mathscr{M} \subset 2^S \) は\(\sigma\)-集合族であるとは限りません.
そのため,集合族 \(\mathscr{M}\) が与えられたとき,それを含むような\(\sigma\)-集合族が存在するか?という問題が湧きます.
この問題に対し,以下の命題が成り立ちます.
命題4.(最小の \(\sigma\)-集合族)\(\mathscr{M} \subset 2^S\) とする. このとき, \(\sigma[\mathscr{M}]_S := \bigcap_{\mathscr{A} \subset 2^S: \sigma\text{-集合族},\ \mathscr{M} \subset \mathscr{A}}\ \ \ \mathscr{A}\) は \(\mathscr{M}\) を含む最小の \(\sigma\)-集合族である.
proof まず,上のような \(\mathscr{A}\) はべき集合 \(2^S\) が存在するため少なくとも1つは存在することに注意. \(\sigma[\mathscr{M}]\) が \(\sigma\)-加法族になること,最小であることの証明は,例えば,「ルベーグ積分入門 --使うための理論と演習」参照.
命題4から,以下の重要な \(\sigma\)-加法族を定義できます.
定義5.(ボレル集合族) \((\mathbb{R}^n, d)\): \(n\) 次元ユークリッド空間,\(\mathcal{O}_d\): 距離位相 とする. \(\mathscr{B}(\mathbb{R}^n) := \sigma[\mathcal{O}_d]_{\mathbb{R}^n}\) をボレル集合族と呼ぶ.
命題6. \((\mathbb{R}^n, d)\): \(n\) 次元ユークリッド空間,\(\mathcal{O}_d\): 距離位相, \(\mathcal{F}_d\): 距離位相に対する閉集合系とする. このとき,\( \mathcal{F}_d \subset \mathscr{B}(\mathbb{R}^n) \) が成り立つ.
proof \(\mathcal{F}_d\) の元は \(\mathcal{O}_d\) のある元の補集合であり,\(\mathcal{O}_d \subset \mathscr{B}(\mathbb{R}^n) \) より,\(\sigma\)-加法族の性質から従う.
上の命題は「閉集合もボレル集合族の中に含まれているよ」と言っています.
さらに,最小の \(\sigma\)-加法族について以下の命題が成り立ちます.
命題7. \(\mathscr{M} \subset 2^S, T \subset S \) とする. このとき,以下が成り立つ: \( \sigma[\mathscr{M}]_S|_T = \sigma[\mathscr{M}|_T]_T\), ここで,\(\sigma\)-加法族 \(\mathscr{A}\) に対し,\( \mathscr{A}|_T := \{ T \cap A | A \in \mathscr{A}\}\) である.
proof
例えば,「ルベーグ積分入門 --使うための理論と演習」参照.
つまり,上の命題は「\(\sigma\)-加法族を作ってから部分集合に制限しても,部分集合に制限してから\(\sigma\)-加法族を作っても,どっちでも結果は同じだよ」と言っています.
そして,上の命題から,ボレル集合族の制限として次の集合を定義します.
定義8. \([0, \infty) \subset \mathbb{R}\) に対し,\( \mathscr{B}([0, \infty)) := \mathscr{B}(\mathbb{R})|_{[0, \infty)}\) と定義する.
いきなりボレル集合族という概念が出てきて困惑したかもしれません.
この概念を考えるモチベーションの1つとして実数値関数の測度による積分が上げられるかと思います.
測度による積分は次回の記事で紹介しますが,可測関数に対して定義されるものになります.
そうすると,可測関数を考える必要があるので,実数値空間に \(\sigma\)-加法族を導入して可測空間にする必要があります.
このとき,どのような \(\sigma\)-加法族を入れると良いか?と言うのが問題として現れますが,その回答の1つがボレル集合族です.
本記事では書き切れないのですが,ボレル集合族は開集合・閉集合を含んでいることから,位相と測度が関連する面白い性質を満たす場合があって,例えば,「ボレル集合族に良い性質の測度が定義されているとき,有限の測度を持つ可測集合は下からコンパクト集合で上から開集合で近似できる」と言う主張が成り立ちます.
少し深入りしましたが,「開集合と閉集合という性質の良い集合を含んだある種自然な \(\sigma\)-加法族」ぐらいの認識で大丈夫かと思います.
定義8は後々使うのですが,積分を定義するときに \( \mathbb{R}\)-値関数を \([0, \infty)\)-値関数の差として分解し,\([0, \infty)\)-値関数(正確には可測関数.この後定義します.)に対して積分を定義し,その差を取ることで元の関数に対して積分を定義するということを行うために必要になります.
可測写像と単関数
測度による積分を考える際に重要な概念である可測写像と単関数を定義します.
定義9.(可測写像)\((S_1, \mathscr{A}_1), (S_2, \mathscr{A}_2)\): 可測空間とする. 写像 \(f: S_1 \to S_2\) が次の性質を満たすとき,\(f\) を \(\mathscr{A}_1/\mathscr{A}_2\) 可測写像(or 単に可測)と呼ぶ: (i) For \(\forall A \in \mathscr{A}_2\), \(f^{-1}(A) \in \mathscr{A_1}\).
可測関数に対して,次の命題が成り立ちます.
命題10. (合成関数の可測性)\((S_1, \mathscr{A}_1), (S_2, \mathscr{A}_2), (S_3, \mathscr{A}_3)\): 可測空間, \(f:S_1 \to S_2, g: S_2 \to S_3\): 可測関数とする. このとき,\( g \circ f: S_1 \to S_3\) は \(\mathscr{A}_1/\mathscr{A}_3\) 可測である.
proof
加速関数の定義を繰り返し用いれば分かる.
「可測関数は合成しても可測だよ」と主張しています.
これは,確率論の期待値計算を考えるときに知っておくと理解が深まる命題だと思います.
次に,非負単関数を定義します.
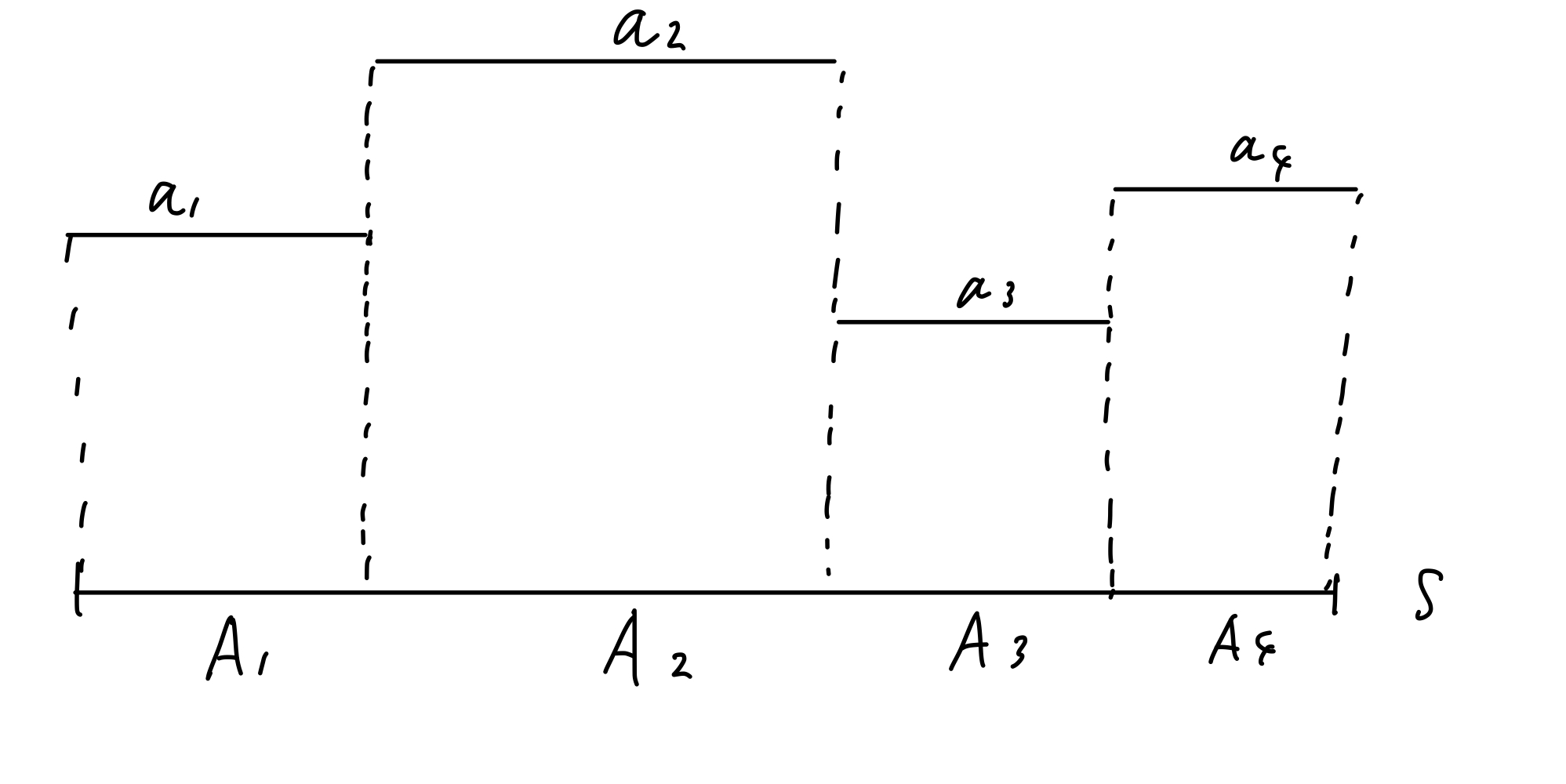
定義11. (非負単関数) \((S, \mathscr{A})\):可測空間とし,\(([0, \infty), \mathscr{B}([0, \infty)))\) を考える. 関数 \( f: S \to [0, \infty) \) が以下の性質を満たすとき,\(f\) は非負単関数であると呼ばれる: (i) \( \exists \{a_n\}_{n=1}^N \subset [0, \infty), \exists \{A_n\}_{n=1}^N \subset \mathscr{A}\ \text{s.t.}\ S = \sum_{n=1}^N A_n, f = \sum_{n=1}^N a_n 1_{A_n} \), ここで,\(1_A\) は集合A上の定義関数である.
単関数は有限個の段差で表されるような関数のことです.
イメージ的には以下です.
また,以下の命題が成り立ちます.
命題12. (非負単関数の可測性) \((S, \mathscr{A})\):可測空間とし,\(([0, \infty), \mathscr{B}([0, \infty)))\) を考える このとき,任意の非負単関数 \( f: S \to [0, \infty) \) は \(\mathscr{A}/\mathscr{B}([0, \infty))\)-可測である.
proof \(f\) による可測写像の引き戻しは,定義から \(f = \sum_{n=1}^N a_n 1_{A_n}\) と表せることにより,可測集合 \(\{A_n\}_{n=1}^N \subset \mathscr{A}\) の有限和で表せるので可測集合である.
そして,可測関数と単関数の関係について,積分を考える上で重要な以下の性質が成り立ちます.
命題13. \((S, \mathscr{A})\):可測空間とし,\(([0, \infty], \mathscr{B}([0, \infty]))\) を考える. 関数 \( f: S \to [0, \infty]\) について,以下は同値である: (i) \( f \) は \(\mathscr{A}/\mathscr{B}([0, \infty])\)-可測 (ii) \( \exists \{f_n\}_{n\geq1}:\text{非負単関数} \ \text{s.t.}\ f_n \nearrow f\) ここで,\(f_n \nearrow f \stackrel{\text{def}}{\Leftrightarrow} f_n(x) \leq f(x)\ \text{for}\ \forall n \in \mathbb{N}, \forall x \in S\), \( \lim_{n\to\infty} f_n(x) = f(x) \ \text{for}\ \forall x \in S\)
proof 例えば,「ルベーグ積分入門 --使うための理論と演習」参照. ※ 証明のイメージは以下に簡単に記載します.
可測写像は語弊を恐れずに言うと測度版の連続写像と考えることができます.
つまり,連続写像は位相を引き戻すと言う性質で定義されましたが,ここでは連続性を考える代わりに可測性を考えているため,可測集合を引き戻すと言う性質で定義されているとみなせるかと思います.
単関数の重要性はまだ今ひとつ分からないかと思いますが,測度による積分を定義するときに単関数についての積分を定義する事が測度による積分のスタート地点になります.これは次回の記事で紹介します.
ルベーグ積分のイメージ図で「横に切って積分する」と言う言葉を聞いたことがある方もいらっしゃるかもしれませんが,あれをもう少し厳密に述べると「可測写像を単関数で近似して,単関数の積分の上限として可測写像の積分を定義する」となります(これも次回紹介します.)
つまり,単関数と言う概念は測度による積分において重要な概念です.
命題13は非負可測関数が非負単関数で下から近似できることを主張しています.
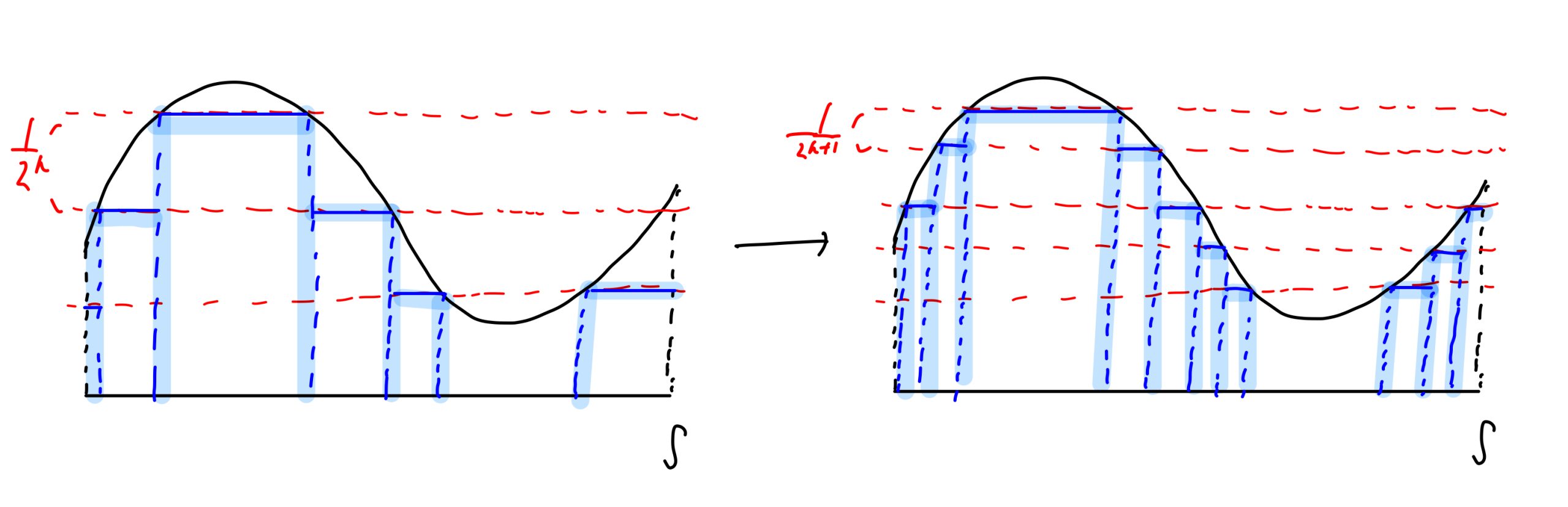
これの直感的な解釈は例えば以下のようなイメージです:
幅 \( \frac{1}{2^n}\) の有限個の区間を取って,以下のイメージのように単関数で近似します.
次に区間幅をさらに \(\frac{1}{2}\) 倍した区間を考え,同様に近似します.
このように近似列を作り区間幅をどんどん小さくしていくと最終的に元の関数に各点で収束するような単関数列が作れます.
命題13の証明はこれを厳密かすることで行えます.
単関数の定義で \(\mathbb{R}\) ではなく,\([0, \infty)\) を考えていることに疑問を持つ方もいるかもしれません.
1つ前の章でも記述しましたが,\(\mathbb{R}\)-値可測関数を \([0, \infty)\)-値可測関数の差に分解して積分を定義します.
なので,\([0, \infty)\)-値について考えれば十分というわけです.
ここで,「本当に\(\mathbb{R}\)-値可測関数を \([0, \infty)\)-値可測関数の差に分解できるの?」という疑問を持つ方もいらっしゃると思います.
これに関して,次の章で肯定的な答えを与えます.
実数値可測関数の性質
ここでは,特に実数値可測関数について成り立ついくつかの主張を紹介します.
命題14. (連続関数の可測性)\(f: \mathbb{R}^n \to \mathbb{R}\):連続とする.
このとき \(f\) は \(\mathscr{B}(\mathbb{R}^n)/\mathscr{B}(\mathbb{R})\)-可測である.
proof 連続関数は開集合を開集合に引き戻すから,ボレル集合族の定義より可測.
命題15. (可測性の保存) \((S, \mathscr{A})\):可測空間とし,\((\mathbb{R}, \mathscr{B}(\mathbb{R}))\),\( f, f_1, f_2 : S \to \mathbb{R}\) : 可測関数とする. このとき,\(-f_1, f_1+f_2, f_1f_2, \text{min}\{f_1, f_2\}, \text{max}\{f_1, f_2\}\) は \(\mathscr{A}/\mathscr{B}(\mathbb{R})\)-可測である. ここで,\(\text{min}\{f_1, f_2\}(x) := \text{min}\{f_1(x), f_2(x)\}\) for \(\forall x \in S\) である(max も同様).
特に,定数関数は可測であるので,\(f^+ := \text{max}\{f, 0\}, f^-:=\text{max}\{-f, 0\}\) は \(\mathscr{A}/\mathscr{B}(\mathbb{R})\)-可測である.
さらに,\(f^+(S), f^-(S) \subset [0, \infty) \) だから,\(f^+, f^-\) は \(\mathscr{A}/\mathscr{B}([0, \infty)) \)-可測であり,\(f = f^+ - f^-\) である.
proof 例えば,「ルベーグ積分入門 --使うための理論と演習」参照.
命題15から,任意の \(\mathbb{R}\)-値可測関数は \([0, \infty)\)-値可測関数の差で表されることが分かります.
命題14は連続関数が可測関数であることを保証しています.
次回の記事で測度を用いた積分を定義するのですが,これは可測関数に対して定義されます.
命題14から,連続関数なら可測関数なので,連続関数に対しても測度を用いた積分が定義できることが分かります.
測度の押し出し
命題16.(測度の押し出し)\((S_1, \mathscr{A}_1, \mu)\): 測度空間,\((S_2, \mathscr{A}_2)\): 可測空間,\(f: S_1 \to S_2\) : \(\mathscr{A}_1/\mathscr{A}_2\)-可測写像とする. このとき, \( \mu_f(B) := \mu(f^{-1}(B))\ \text{for}\ \forall B \in \mathscr{A}_2 \) で定まる写像 \(\mu_f\) は\(\mathscr{A}_2\) 上の測度となる. これを可測写像 \(f\) による測度 \(\mu\) の押し出しと呼び,\(\mu_f\) を \(f\) による \(\mu\) の押し出し測度(像測度)と呼ぶ.
proof逆像の性質と \(\mu\) が測度であることを用いると \(\mu_f\) が測度の定義を満たすことが分かる.
上の命題は既に測度が定まっている空間 \( (S_1, \mathscr{A}_1, \mu) \) からまだ測度が定まっていない空間 \((S_2, \mathscr{A}_2)\) に可測写像を使うことで測度を定められることを述べています.
確率変数の分布は,まさに,確率変数という可測写像による押し出し測度のことです.
終わりに
本記事では,可測空間と測度の定義から始めて,可測写像と単関数の関係や可測関数に対して成り立つ性質について紹介しました.
これで,測度による積分を定義するための準備が完了したので,24日目の記事で測度を用いた積分と成立するいくつかの命題について紹介する予定です.
本記事の内容は私の個人的な考えに基づいて絞っているため,測度論のトピックの中で扱えていないものが多々あります.
本記事で扱っていないトピックが載っていておすすめの本として以下を挙げさせていただきます(私はこの本で測度論を一通り勉強しました):
- 新装版 ルベーグ積分入門 --使うための理論と演習,吉田伸生先生著
ここまで読んでいただきありがとうございました.
明日は開発チームの市村から【React Flowを使ってみた】というタイトルで記事が出る予定です.
そちらもご覧いただけますと幸いです.






